Tree - 이진 검색 트리 - 3
이어서 delete 연산이다.
delete가 3개의 연산중에 가장 복잡한데,
경우에 따라 연산이 다르기 때문이다.
첫번째는 자식이 없을 때이다.
자식이 없을 때는 노드를 그냥 삭제한다.
두번째는 하나의 자식이 있는 경우이다.
이 경우는 링크드 리스트에서 가운데 값을 하나 삭제하는 것과 비슷하므로
간단하게 처리할 수 있다.
7을 삭제하고 노드 6의 포인터를 13을 가리키도록 해주면 된다.
마지막으로 자식을 둘인 노드를 삭제하는 경우이다.
이것이 delete 연산의 가장 복잡한 경우이다
노드 13을 삭제하는 경우, 13을 그냥 없애 버리면 자식 노드의 부모가 없어지므로
노드 13의 저장된 데이터(13)만 삭제한다.
이후에 없어진 데이터의 successor를 삭제된 부분으로 옮겨온다.
이렇게 하면 트리 전체의 크기 관계가 훼손되지 않는다.
그 다음, succesor는 자식 노드가 없거나 하나 있으므로
예시 1번이나 2번의 방법으로 처리해 주면 된다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | TREE-DELETE(T,z){ if left[z] = null or right[z] = null then y <- z else y <- TREE-SUCCESOR(z) if left[y] != null then x <- left[y] else x <- right[y] if x != null then p[x] <- p[y] if p[y] = null then root[T] <- x else if y = left[p[y]] then left[p[y]] <- x else right[p[y]] <- x if y != z then key[z] <- key[y] copy y`s satelite data into z return y } | cs |
삭제 연산의 슈도 코드는 다음과같다.
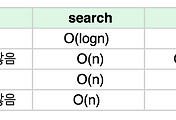
이때의 시간 복잡도 역시 다른 연산과 마찬가지로
O(h)가 되며, 높이에 비례한다.
그 뜻은 최악의 경우일 때 시간 복잡도가 O(n)이 된다는 것이다.
이를 해결해주기 위해서 균형(balanced)잡힌 트리를 사용하며
균현 잡힌 트리는 키의 삽입이나 삭제시 추가로 트리의 균형을 잡아줌으로써
높이를 O(log_2(n))으로 유지한다.
물론 추가, 삭제 등의 연산이 기본 이진 트리보다 다소 복잡해진다.
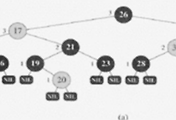
균형잡힌 트리의 예로는 레드 블랙트리가 있다.
따라서 다음은 레드 블랙트리에 대해서 알아보자
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Tree - 레드 블랙 트리(Red Black Tree) - 2 (0) | 2017.04.19 |
|---|---|
| [알고리즘] Tree - 레드 블랙 트리(Red Black Tree) - 1 (0) | 2017.04.19 |
| [알고리즘] Tree - 이진 검색 트리 - 2 (0) | 2017.04.19 |
| [알고리즘] Tree - 이진 검색 트리 - 1 (0) | 2017.04.19 |
| [알고리즘] Tree - 트리와 이진트리 (0) | 2017.04.19 |






댓글