Tree - 이진 검색 트리 - 1
검색 트리라는 것은 트리라는 자료구조를 이용하여
순회하며 데이터를 검색하는 것이다.
트리는 계층적인 구조를 가지고 있으나,
검색트리는 일종의 컨테이너나 집합이라고 볼수있다.
따라서 이를 다이나믹 셋(dynamic set)이나 딕셔너리(dictionary),
검색 구조(search structure)라고도 부른다.
데이터들이 고정되지 않고 새로운 데이터의 추가/삭제가 가능한것이 특징이다.
다이나믹 셋의 조건은 다음과 같다.
여러개의 키를 저장하고 있으면서
insert/search/delete가 가능하다.
연결리스트와 배열을 정렬되어지거나 정렬되어지지 않거나에 대한
비교는 위의 표와 같다.
연결 리스트나 배열을 썼을 때, 위의 표에서 알수 있는 점은
search, insert, delete중에 적어도 하나는 O(n)의 시간을 피할수 없다는 것이다.
이 3가지 연산을 셋 다 동시에 위의 표보다 효율적으로 할수 있는 방법은 없을 것 인가에 대한 연구가 60~70년대 주로 연구되어지던 알고리즘이다.
그 해답중 첫번째는 탐색 트리(Search Tree)이며
두번째는 해슁(Hashing)이 된다.
탐색트리는 일반적으로 Search, Insert, Delete의 기능을
효과적으로 수행하기 위해서 사용되며
보통 Search, Insert, Delete는 해당 트리의 높이에 비례하는 시간 복잡도를 가진다.
레드블랙트리나 AVL트리, B-트리 등은
이진 트리의 아이디어를 조금더 확장하거나 발전시킨 알고리즘이다.
때문에, 탐색 트리중에서 가장 기본적인 이진 트리를 알아보도록 하자
이진 검색 트리는 BST(Binary Search Tree)라고 불린다.
이름 그대로 이진 트리이며 각 노드에 하나의 키를 저장한다.
또한 다음의 조건도 만족해야하는데,
각 노드 v에 대해서 그 노드의 왼쪽 서브트리에 있는 키들은 key[v]보다 작거나 같고
오른쪽 서브트리에 있는 값은 크거나 같다.
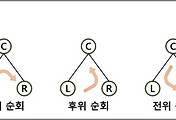
위의 왼쪽 그림을 보면
임의의 노드에 대해서 왼쪽 서브트리에 있는 키들은 임의 노드의 값보다 작거나 값고
오른쪽 서브트리에 있는 값은 크거나 같음을 알 수 있다.
오른쪽 그림도 이진 검색 트리이다.
여기서 binary heap과 헷갈릴수 있는데
이진 검색트리는 binary heap와 다르게
complete binary tree와 같은 모양의 제한이 없다.
다음으로 연산에 대한 예제를 보도록 하자
위의 그림은 13을 찾는 예제이다.
우선적으로 root 노드로 접근하여 해당 데이터가 13인지 확인한다.
root 노드의 데이터가 13보다 크다면 왼쪽, 작거나 같다면 오른쪽으로 이동한다.
밑으로 내려간 후 타겟이 나올때 까지 같은 작업을 반복한다.
1 2 3 4 5 6 7 8 | TREE-SEARCH(x,k){ if x= null or k=key[x] then return x if k < key[x] then return TREE-SEARCH(left[x],k) then return TREE-SEARCH(right[x],k) } | cs |
이를 슈도 코드로 표현하면 다음과 같다.
먼저 트리에 값이 없을 경우와 값을 찾았을 경우 리턴을 해준다.
그렇지 않을 경우 재귀적으로 값이 나올 때 까지 왼쪽/오른쪽 트리를 검색해 나간다.
여기서 시간복잡도는 O(h)이며 시간복잡도는 높이에 비례한다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Tree - 이진 검색 트리 - 3 (0) | 2017.04.19 |
|---|---|
| [알고리즘] Tree - 이진 검색 트리 - 2 (0) | 2017.04.19 |
| [알고리즘] Tree - 트리와 이진트리 (0) | 2017.04.19 |
| [알고리즘] Sort - Java에서의 정렬 (Sort in java) (0) | 2017.04.19 |
| [알고리즘] Sort - Radix sort와 정렬의 속도 비교 (0) | 2017.04.19 |





댓글