Tree - 이진 검색 트리 - 2
1 2 3 4 5 | TREE-MINIMUM(x){ while left(x) != null do x <- right[x] return x } | cs |
이진 검색 트리의 간단한 기본적인 예를 살펴보자
첫 번째로 최소값 찾기이다.
간단하게 생각했을때 이진 검색트리의 최소 값은
루트에서 출발하여 왼쪽을 따라 쭉 내려갔을 때 가장 마지막 노드(leaf)가 된다.
이를 슈도 코드로 표현하면 위의 코드와 같다.
다음 예제는 successor이다.
일반적인 배열에서 successor는 바로 다음값,
predeccesor는 바로 전값이다.
이진 트리에서는 바로 다음 크기값이 successor,
바로 전 크기 값이 preccesor가 된다.
모든 키들이 서로 다르다고 가정해야지 successor용어가 명확하게 정의 된다.
successor에는 3가지 규칙이 존재하는데
1) 노드 x의 오른쪽 서브트리가 존재하는 경우, 오른쪽 서브트리의 최소값
2) 오른쪽 서브트리가 존재하지 않을때, 어떤 노드 y의 왼쪽 서브트리의 최대값이 x가 되는 노드 y가 x의 successor
3) 위의 예 2번의 노드 y가 존재가 하지 않을 경우 successor가 존재 하지 않는다.
1 2 3 4 5 6 7 8 9 10 | TREE-SUCCESOR(x){ if right[x] != null then return TREE-MINIMUM(right[x]) y <- p[x] while y != null and x = right[y] do x <- y y <- p[y] return y } | cs |
이것이 이진 검색 트리의 슈도 코드이다.
시간 복잡도는 TREE-MINIMUM과 마찬가지로 O(h)이다.
이진 검색에서 중요한 연산은 insert, search, delete 라고 했는데
그중 insert에 대해 알아보자
insert는 새로운 노드를 이진 검색 트리에 추가하는 연산이다
새로운 노드를 추가할 때 기존의 노드들은 전혀 건드리지 않는다.
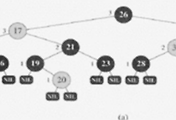
따라서 14를 추가 할때 root 값과 비교하여 왼쪽/오른쪽 방향을 정한다.
15보다 작으므로 왼쪽으로 내려가고 다시 6과 비교,
6보다 크므로 오른쪽으로 내려가고 7과 비교,
7보다 크고 그 하위의 13보다도 크기때문에
14는 13의 오른쪽 노드에 삽입된다.
위의 예는 empty tree에 6개의 데이터를 넣어주는 과정이다.
[30,20,25,40,10,35]의 순서로 삽입된다.
삽입 연산의 특징은 기존의 노드들을 건드리지 않는것인데
그림에서도 먼저 들어간 데이터가 변화하지 않는것을 알 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | TREE-INSERT(T,z){ y <- null x <- root[T] while x != null do y <- x if key[z] < key[x] then x <- left[x] else x <- right[x] p[z] <- y if y = null then root[T] <- z else if key[z] < key[y] then left[y] <- z else right[y] <- z } | cs |
따라서 삽입 연산을 슈도 코드로 작성하면 위와 같다.
비교를 통해 노드가 삽입될 자리를 찾아가며 해당 자리에 노드를 삽입해 주게 된다.
시간 복잡도는 역시 O(h)가 된다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Tree - 레드 블랙 트리(Red Black Tree) - 1 (0) | 2017.04.19 |
|---|---|
| [알고리즘] Tree - 이진 검색 트리 - 3 (0) | 2017.04.19 |
| [알고리즘] Tree - 이진 검색 트리 - 1 (0) | 2017.04.19 |
| [알고리즘] Tree - 트리와 이진트리 (0) | 2017.04.19 |
| [알고리즘] Sort - Java에서의 정렬 (Sort in java) (0) | 2017.04.19 |




댓글