Sort - Heap의 응용, 우선 순위 큐(Priority queue)
큐는 여러개의 데이터를 넣을수 있는 컨테이너이다.
데이터가 들어오고 나갈때는
First In First Out(FIFO) 구조를 가진다.
우선 순위 큐는 이러한 큐의 한종류로써
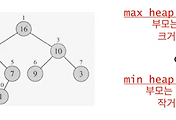
최대 우선 순위 큐와 최소 우선 순위 큐로 나뉜다.
우리는 최대 우선 순위 큐를 중심으로 알아보도록 하겠다.
최대 우선순위큐는 다음의 두가지 연산을 지원하는 자료구조이다.
1) INSERT(x) : 새로운 원소 x 를 삽입
2) EXTRACT_MAX : 최대값을 삭제하고 반환
반대로 최소 우선 순위큐는 EXTRACT_MAX대신 EXTRACT_MIN을 지원한다.
MAX HEAP을 이용해서 최대 우선 순위 큐를 구현할 수있다.
먼저 INSERT에 대해서 알아보도록 하자
위의 그림은 MAX HEAP의 형태로 저장되있는 우선순위 큐이다.
현재 heap의 상황은
1) Complate binary tree
2) Max heap property
를 만족하므로 이를 유지하면서 INSERT 연산을 하기위해서는 고려할 사항들이 있다.
INSERT는 새로운 노드를 추가해야하는데 complate binary tree 만족하려면
가장 마지막 레벨의 leaf에 추가 될수 밖에 없다.
그러나 이 추가 연산이 끝나면 max heap property를 만족하지 못한다.
따라서 heap sort를 이용해서 전체 heap을 정렬시키고
max heap property를 만족시키도록 해야한다.
1 2 3 4 5 6 7 8 9 | MAX-HEAP-INSERT(A, key){ heap_size = heap_size+1; A[heap_size] = key; i = heap_size; while(i>1 and A[PARENT(i)] < A[i]){ exchange A[i] and A[PARENT(i)]; i= PARENT(i); } } | cs |
슈도 코드로 MAX-HEAP-INSERT를 나타내었다.
위의 코드에서 A가 HEAP이다.
heap의 사이즈를 1 증가 시켜 주고 그 자리에 새로운 key값을 넣어준다.
i는 문제 노드(새로 추가된)의 인덱스이다.
그 후 while문에서 i>1이라는것은 root 노드가 아니라는 뜻이며
A[PARENT(i)]<A[i] 부모 노드에 저장된 값보다 크다는 것이다.
위의 조건에 해당된다면 부모 노드와 값을 교환해준다.
다시말해 root노드가 될때까지 또는, 자신의 부모 노드보다 작을 때까지
교환연산을 진행하게 되는 것이다.
이때 시간 복잡도는 트리에 높이에 비례하게 되나
heap은 complete binary tree이므로 O(nlogn이다.)
다음은 EXTRACT_MAX를 표현한 그림이다.
heap은 complete binary tree이므로 아무 노드나 삭제할 수 없다.
여전히 complete binary tree를 만족하기 위해서는
마지막 노드(6)를 삭제할 수 밖에 없다
따라서 root노드 값을 삭제하고 마지막 노드를 삭제 후
마지막 노드에 있던 값을 root노드로 옮겨주게 된다.
이 후 heap property 복원을 위해서 sort를 진행하게 된다.
1 2 3 4 5 6 7 8 9 | HEAP-EXTRACT-MAX(A){ if heap-size[A]<1 then error "heap underflow" max <- A[1] A[1] <- A[heap-size[A]] heap-size[A] <- heap-size[A]-1 MAX-HEAPIFY(A,1) return max } | cs |
EXTRACT-MAX의 슈도코드이다.
size가 1보다 작을경우 dequeue연산을 진행할 수 없으므로 에러메세지를 출력한다.
그렇지 않으면 A[1]의 값(root)을 리턴하기 위해 max에 넣어준다.
이 후 마지막 값을 루트로 이동 시켜준 후 마지막 노드를 삭제한다.
마지막으로 sort 함수를 호출하면 EXTRACT-MAX연산이 완료된다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Sorting in leanar time(선형시간 알고리즘) (1) | 2017.04.19 |
|---|---|
| [알고리즘] Sort - 정렬의 Low Bound (0) | 2017.04.19 |
| [알고리즘] Sort - 힙정렬(heap sort) - 2 (0) | 2017.04.19 |
| [알고리즘] Sort - 힙정렬(heap sort) - 1 (0) | 2017.04.19 |
| [알고리즘] Sort - 퀵정렬(Quick sort) (0) | 2017.04.19 |




댓글