Sort - 정렬의 Low Bound
앞서 여러가지 정렬을 살펴보았다.
그 결과 다음과 같은 질문을 할수 있을것 가다.
과연 O(nlogn)이라는 시간복잡도가 최선일까
미리 결론을 이야기하자면
O(nlogn)보다 더 나은 시간복잡도는 없다는 것이다.
여기에는 한가지 전제조건이 붙는데
Comparison sort(비교 정렬)에 대해서는 ![]() 보다 더 나은 복잡도가 없다는 것이다.
보다 더 나은 복잡도가 없다는 것이다.
그렇다면 comparison sort는 무엇일까
comparison sort는 데이터와의 크기 관계만을 이용해서 정렬하는 알고리즘이다.
따라서 데이터들의 크기관계가 정의되어있다면 어떤 데이터 형 에서도 적용이 가능하다
(문자, 알파벳, 사용자 정의 객체 등)
따라서 앞서 살펴본 버블, 삽입, 선택, 퀵, 힙 정렬들이 모두 해당된다고 볼 수 있다.
이와 반대되는 개념은 non-comparison sort이며
정렬된 데이터에 대한 사전 지식을 이용하기 때문에 적용에 제한이 있다.
Bucket sort나 Radix sort등이 이에 해당한다.
그래서, 이 포스팅의 주제는
어떤 Comparison sort의 시간 복잡도도 O(nlogn)을 넘지 않는다는 것을
증명하는 것이다.
따라서 어떤 좋은 Comparison sort도 ![]() 을 넘지 않기 때문에
을 넘지 않기 때문에
이와 같은 개념을 '하한' 이라고 한다.
이를 위해서 decision tree라는 것을 이용해서
하한에 대해서 알아보도록 하자
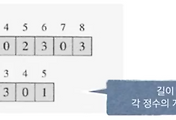
위의 그림은 Insertion sort에 대한 예제인데,
decision tree는 이러한 과정을 하나의 tree로 나타낸 것이다.
정렬할 데이터가 a(1),b(2),c(3)라면
맨처음(root) 순서는 a(1)와 b(2)를 비교하는 것이다.
이에 따라 선택지는 2개로 분화되게 된다.
a(1)가 큰 경우와 b(2)가 큰 경우이다.
이와 같이 데이터를 비교할 때, 데이터 값에 따라 나오는 경우의 수가 여러가지 이다.
이 decision tree에서 leaf 노드는 n!개이다.
왜냐하면 모든 순열에 해당하기 때문이다.
따라서, decision tree를 이용해 구해본 최악의 경우 시간 복잡도는
이 트리의 높이에 비례한다.(비교 연산)
그렇다면 이진 트리에서 leaf node가 n!일 때 트리의 높이는
height >= ![]() = O(
= O(![]() ) 이 된다.
) 이 된다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Sort - Radix sort와 정렬의 속도 비교 (0) | 2017.04.19 |
|---|---|
| [알고리즘] Sorting in leanar time(선형시간 알고리즘) (1) | 2017.04.19 |
| [알고리즘] Sort - Heap의 응용, 우선 순위 큐(Priority queue) (0) | 2017.04.19 |
| [알고리즘] Sort - 힙정렬(heap sort) - 2 (0) | 2017.04.19 |
| [알고리즘] Sort - 힙정렬(heap sort) - 1 (0) | 2017.04.19 |






댓글