최소비용신장트리(Minimum Spanning Tree) - 1
최소 신장트리는 다양한 분야에서 응용되는 가장 기본적인 그래프 문제이다.
보통 네트워크(통신, 도로, 가스배관 등) 디자인과 같이 뭉뚱그려서 말하는데
연결되어 있으면서 비용이 최소화 된다는 것은 모든 종류의 네트워크에서 요구되어지는 것이기 때문이다.
또한 이미지 프로세싱과 같은 분야에서도 이와 같은 알고리즘을 많이 사용된다.
구체적인 예를 들자면, N개의 도시가 있고 도시와 도시를 연결하는 도로의 비용 W가 있다.
위의 그래프에서 정점들이 도시들이고 엣지의 weight가 비용이라고 가정한다.
엣지가 없는 경우에는 어떠한 이유로 두 도시를 직접 연결하는 도로를 만드는것이 불가능하거나
그 비용이 무한대라고 가정한다.
예산이 충분하다면 모든 도시간의 도로를 만들수 있지만, 이는 불가능하므로,
최소의 비용을 가지고 모든 도시들이 연결되도록 하는 방법을 구할 때 최소 비용 신장 트리 문제 라고한다.
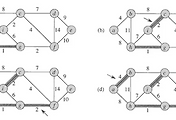
가장 위에서 본 예에서 최소 비용 신장 트리는 다음 그림과 같다.
한가지 중요한 사실은 최소 비용 신장 트리의 해는 유일하지 않다.
예를 들어 (b, c) 대신 (a, h)를 사용해도 된다.
이 때, 그래프의 조건은 다음과 같다.
1. 무방향 가중치 그래프
2. 각 노드 (u,v)에 대해 가중치 w(u,v)가 있으며
그리고 문제를 해결하기 위해서
1. 모든 노드들이 서로 연결된다.
2. 가중치의 합이 최소가 된다.
위의 조건을 만족해야한다.
한 가지 의문점이 드는것이, 이것을 왜 '트리'라고 부르는 것일까.
보통 트리라고 하면 계층적인 구조를 말하는데, 사실은 트리라는 말은 맥락에 따라 다른 정의를 가지기도 한다.
일반적으로, 공학분야에서는 계층적 구조를 트리라고 부르지만
수학 분야에서는 트리가 '사이클이 없는 무방향 그래프'를 뜻한다.
위의 그림을 보면 모든 노드들이 연결되어있다.
또한 다시 자기 자신으로 돌아올 수 있는 사이클이 없다.
따라서 위의 그림은 트리이다.
그러므로 최소 신장 트리에서는 사이클(중복 연결)이 만들어 질 수 없다.
1 2 3 4 5 6 7 | Generic-MST(G, w){ A<-ø while A does not form a spanning tree do find edge (u,v) that is safe for A A<-A U {(u,v)} return A } | cs |
크루스칼과 프림의 알고리즘이 가장 유명한 MST의 알고리즘이다.
이 알고리즘이 가지고 있는 공통적인 부분이 있는데 이를 Generic MST 알고리즘이라고 하자.
Generic MST로 본질적인 접근법이나 구조등을 생각해보고 구체적인 두가지 알고리즘을 파악할 것이다.
Generic MST는 다음과 같다.
어떤 A에 대해서 A U {(u,v)}도 역시 어떤 MST의 부분 집합이 될 경우
에지(u,v)는 A에 대해서 안전(safe)하다고 한다.
1. 처음에는 A=ø 이다
2. 집합 A에 대해서 안전한 엣지를 하나 찾은 후 이것은 A에 더한다
3. 엣지의 개수가 n-1개가 될 때 까지 2번을 반복한다.
그렇다면 문제는 어떻게 안전한 엣지를 찾을것이냐 이다.
이를 위해서 먼저 몇가지 생소한 용어의 정의를 해보자
1. 그래프의 정점들을 두개의 집합 S와 V-S로 분할한 것을 컷(cut) (S,V-S)라고 부른다.
2. 엣지 (u,v)에 대해서 u->S이고 v->V-S 일 때 엣지 (u,v)는 컷 (S, V-S)를 cross한다고 말한다.
3. 엣지들의 부분 집합 A에 속한 어떤 엣지가 컷 (S, V-S)를 cross 하지 않을 때 컷 (S,V-S)는 A를 존중한다(respect)고 한다.
용어에 대한 상세한 설명은 위의 그림을 참고하도록 하자
이러한 용어가 기반이 되어야 뒤에 나오는 내용이 쉽게 설명 될 수 있다.
정리를 하자면, A에 대해서 안전하다는 것은 다음과 같다.
위의 그림에서 빨간 엣지를 A라고 할 때,
A가 어떤 MST의 부분집합이고 (S, V-S)를 A를 존중하는 컷이라고 하자.
이 컷을 cross하지 않는 에지들 중 가장 가중치가 작은 에지 (u, v)는 A에 대해서 안전하다고 할 수있다.
(여기서 어떤 MST라고 칭하는 이유는 MST가 유일하지 않기 때문)
즉, lightest edge라고 표기된 엣지를 MST의 성분으로 골라도 된다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [Backjoon] 7567번 문제 - 그릇 (0) | 2017.05.26 |
|---|---|
| [알고리즘] 최소비용신장트리(Minimum Spanning Tree) - 2 (0) | 2017.05.25 |
| [알고리즘] DAG와 위상 순서 (0) | 2017.05.24 |
| [알고리즘] 순회 - 그래프에서의 DFS (0) | 2017.05.10 |
| [알고리즘] 순회 - 그래프에서의 BFS (0) | 2017.05.10 |







댓글