DAG와 위상 순서
DAG(대그)란 Directed Acyclic Graph를 뜻한다.
직역하면 '방향성 비 사이클' 그래프이며 방향을 가지되, 루프를 생성하지 않는 그래프를 말한다.
여기서 루프, 또는 사이클이란 자기 자신에서 출발해서 다시 자신에게 돌아오는 경로를 말하며
비 사이클이므로 이러한 경로가 없어야 한다.
위의 그래프에서 엣지들을 따라 가면 어느 경로에서도 자기 자신으로 돌아올 수 없다.
DAG는 중요한 용도를 가지는데,
일반적으로 작업의 우선순위를 표현할 때 DAG의 구조를 가지게 된다.
예를 들면, 집을 지을 때 기초공사나 기둥세우기, 인테리어 등을 해야한다.
이 때, 기둥을 세우기 전에 인테리어를 할 수 없듯이
다른 것 보다 선행 되어야 하는 것들 표현 하기 위해 DAG가 유용하게 사용된다.
만약 이러한 우선 순위를 표현한 그래프에서 사이클이 존재한다면
해당 작업은 영원이 끝나지 못한다.
(닭이 먼저냐 달걀이 먼저냐 처럼, 가장 먼저 시작해야 할 일이 구분되어 지지 않으므로)
DAG에서는 우선순위를 표현하기 위해 위상 정렬을 사용한다.
위상 정렬이란, 작업을 실제로 한번에 하나씩 순서대로 처리한다면
어떤 순서로 작업해야 하느냐를 표현한 것이다.
즉, 작업의 순서대로 노드를 일렬로 정렬하는 것이다.
이러한 위상 정렬을 위해 조건이 있는데,
노드의 순서가 왼쪽에서 오른쪽 방향으로 향해야한다.
역방향 노드가 있다면 올바른 작업의 순서가 될수 없다.
위상 정렬은 시작값에 따라 여러 가지로 표현될 수 있고
결론적으로 답이 하나로 유효하지 않다.
1 2 3 4 5 6 7 8 | topologicalSort1(G){ for <- 1 to n { 진입 간선이 없는 임의의 정점 u를 선택한다. A[i]<-u; 정점 u와 진출간선을 모두 제거한다. } // 배열 A[1...n]에는 정점들이 위상 정렬 되어있다. } |
위의 코드는 첫번째 위상 정렬 알고리즘이다.
알고리즘을 보기에 앞서 그래프에 대한 용어를 정리하자.
방향 그래프에서 들어오는 엣지를 Incomming 나가는 엣지를 Outgoing이라고 한다.
또한, 들어오는 엣지의 개수를 Indegree 나가는 엣지의 개수를 Outdegree라고 한다.
첫번째 위상 알고리즘은 간단하고 직관적이다.
첫째로, 모든 노드들에 대해서 indegree가 0인 노드를 찾는다.
indegree가 0라는 것은 해당 작업에 선행해야 할 작업이 없다는 것을 뜻한다.
2개 이상 존재하면 그중 하나를 선택한다.
그 후, 노드 A와 A에서 나가는 엣지를 그래프에서 제거한다.
그리고 다시, 남은 그래프에서 indegree가 0인 노드를 찾는다.
작업이 끝났으면 해당 노드와 해당 노드에서 나가는 엣지를 그래프에서 제거한다.
이와같은 작업을 반복하면 결론적으로 마지막 노드까지 도달할수 있으며
모든 노드가 위상 정렬된다.
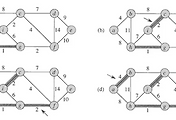
위의 그림은 첫번째 위상 정렬 알고리즘의 예이다.
Indegree가 0인 노드를 찾고 해당 노드를 출력한 후, 링크와 함께 삭제해 나간다.
모든 노드가 사라질 때까지 반복문을 수행한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | topologicalSort2(G){ for each v->V visited[v] <- NO; make an empty linked list R; for each v->V // 정점의 순서는 상관 없음 if(visited[v] = NO) then DFS-TS(v,R); } DFS-TS(v, R){ visited[v] <- YES; for each x adjacent to v do if(visited[x] == NO) then DFS-TS(x,R); add v at the front of the linked list R; } | cs |
두번째 위상 정렬 알고리즘이다.
일단, 모든 노드들에 대해서 visited를 NO로 설정해준다.
아직 아무 노드도 출력 되지 않았다는 뜻이다.
그 후에, 하나의 빈 링크드 리스트 R을 만드는데,
노드를 위상 정렬해서 정렬된 순서대로, 연결 리스트로 노드들을 정렬할 것이기 때문이다.
그리고 아직 방문하지 않은 아무 노드 하나를 잡아서 그 노드에서 출발하는 DFS를 실행한다.
DFS는 방문한 노드를 체크하고 그 노드와 인접한 노드 x에 대해
해당 노드가 방문되지 않았다면 다시 DFS를 실행한다.
그러나 일반적인 DFS와 다른점은 마지막 줄이다.
for 반복문을 빠져 나왔다는 것은 모든 노드를 방문해보고 갈곳이 없을 때 이다.
일반적인 DFS는 뒤로 되돌아 갔으나, 여기서는 링크드 리스트 R에 해당 노드를 추가해준다.
두번째 알고리즘을 실행한 결과이다.
마지막 노드까지 DFS를 실행하고 끝에 도달했을때 링크에 해당 노드를 추가한다.
이렇게 링크에 하나씩 추가를 하며, 방문되지 않는 노드에서 계속해서 DFS를 실행한다면
결국 위상 정렬된 링크드 리스트를 얻을 수 있다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] 최소비용신장트리(Minimum Spanning Tree) - 2 (0) | 2017.05.25 |
|---|---|
| [알고리즘] 최소비용신장트리(Minimum Spanning Tree) - 1 (1) | 2017.05.24 |
| [알고리즘] 순회 - 그래프에서의 DFS (0) | 2017.05.10 |
| [알고리즘] 순회 - 그래프에서의 BFS (0) | 2017.05.10 |
| [알고리즘] 그래프의 개념과 표현 (0) | 2017.05.10 |









댓글