728x90
반응형
Recursion의 응용 - Counting Cells in a Blob
Counting Cells in a Blob(인접한 셀의 개수 찾기)의 조건
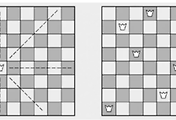
1) 입력으로 하나의 바이너리 이미지가 주어진다(흑백 이미지라고 생각)
2) 각 픽셀은 background pixel(흰색) 이거나 image pixel(파란색)이다
3) 서로 연결된 image pixel들의 집합을 blob이라고 한다.
4. 상하좌우, 대각선 방향도 연결된 것으로 간주
입력
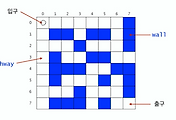
- NxN의 2차원 배열 그리드
- 하나의 좌표(x,y)
출력
- 픽셀(x,y)가 포함된 blob의 크기
- (x,y)가 어떤 좌표에도 속하지 않을 경우에는 0을 리턴
1 2 3 4 5 6 7 8 9 | 현재 픽셀이 속한 blob의 크기를 카운트 하려면 현재 픽셀이 image color가 아니라면 0을 반환한다. 현재 픽셀이 image color라면 먼저 현재 픽셀을 카운트 한다(count=1) 현재 픽셀이 중복 카운트 되는 것을 방지 하기 위해 다른 색으로 칠한다. 현재 픽셀이 이웃한 모든 픽셀들에 대해서 그 픽셀이 속한 blob의 크기를 카운트 하여 카운터에 더해준다 카운터를 반환한다. | cs |
미로찾기와 마찬가지로 이문제를 해결하기 위해서는 재귀적 사고가 필요하다.
재귀적으로 문제를 풀때 위와같은 슈도 코드의 작성이 가능하다.
이웃한 픽셀들을 체크 할때는 북, 북동, 동, 동남... 순으로 한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 | Algorithm for coutCells(x,y) // 유효한 좌표가 아닐 때 if the pixel(x,y) is outside the grid the result is 0; // 백그라운드 픽셀이거나 이미 픽셀이 카운트 된 경우 else if pixel(x,y) is not an image pixel or already counted the result is 0; else set the colour of the pixel (x, y) to a red colour; the result is 1 plus the number of cells in each piece of the bolb that includes a nearest neighbour; | cs |
좀더 구체적인 슈도 코드로 나타내면 다음과 같다.
먼저 유효성을 검사하고 마지막으로 base case에 수렴하도록 한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | private static int BACKGROUND_COLOR = 0; private static int IMAGE_COLOR = 1; private static int ALREADY_COLOR = 2; public int countCells(int x,int y){ int result; if(x<0 || x>=N || y<0 || y>=N) return 0; else if(grid[x][y] != IMAGE_COLOR) return 0; else{ grid[x][y] = ALREADY_COUNTED; result 1 + countCells(x-1,y+1) + countCells(x, y+1) + countCells(x+1,y+1) + countCells(x-1, y) + countCells(x+1,y) + countCells(x-1, y-1) + countCells(x,y-1) + countCells(x+1, y-1); } } | cs |
결과적으로 다음과 같은 코드가 나타난다.
좌표를 입력으로 받으면 우선 그리드 내부에 있는지 유효성을 검사한다.
다음으로 이미 방문했거나, 셀이 background인지를 검사한다.
마지막으로 그것이 아니라면 전방위로 순회하며 count를 검사해서 결과값을 리턴한다.
순회는 재귀로 이루어진다.
출처 : 부경대 권오흠 교수님, 영리한 프로그래밍을 위한 알고리즘
반응형
'알고리즘 문제풀이' 카테고리의 다른 글
| [알고리즘] Recursion의 응용 - 멱집합(power set) (0) | 2017.04.19 |
|---|---|
| [알고리즘] Recursion의 응용 - n queens (0) | 2017.04.19 |
| [알고리즘] Recursion의 응용 - 미로찾기 (0) | 2017.04.18 |
| [알고리즘] Recursion 이란 - 3 (0) | 2017.04.18 |
| [알고리즘] Recursion 이란 - 2 (0) | 2017.04.18 |



댓글